Dans la culture japonaise, les parents partageaient leur connaissances et savoir faire avec leur enfants. L’enfant commence à apprendre ce qu’on appelle des Kata (synonyme de « forme » ou « cadre » en français). On peut penser qu’un enfant d’un menuisier apprendra les Kata du métier du menuisier, et un enfant d’un pianiste apprendra les cadres de l’art pratiqué par ses parents. Un Kata est généralement un jeu dans lequel on passera des connaissances que les enfants s’apprenaient du monde de travail des adultes. En effet, les Kata sont très connus dans le monde des arts martiaux (Karaté, Judo..). Ce concept a attiré l’attention des informaticiens ensuite surtout avec la monté de la méthode agile d’extrême programming (XP) de Kent Beck, dont je suis très enthousiaste :).

Le concept des Kata a été présenté pour le monde de développement informatique par Dave Thomas dans son livre « The pragmatic programmer« . Beaucoup de piliers du craft logiciels comme oncle Bob dans son livre « The clean coder » ou principalement dans son article « The programming Dojo« , Sandro Mancuso dans son livre « The software Craftsman« , et d’autres…, encourageaient les développeurs à pratiquer les kata d’une manière continue afin de perfectionner leur compétences.

Il existe plusieurs Kata, la plus connu que j’enseignais à mes étudiants aux lycées et à l’université c’était les nombres romains. Malheureusement, J’enseignais les problèmes sans savoir qu’ils sont des katas et aussi sans approche TDD, sans pair programming. Bref, l’idée est de résoudre le problème avec une approche impérative sans tests unitaires. Malheureusement, cela ne permettra pas au développeur (étudiant, enseignant) de comprendre l’utilité du problème et de penser aux différents cas de tests possibles.

Ils existent d’autres Kata, comme le célèbre Fizz Buzz, Gilded Rose et plein d’autres. Le site codingDojo, présente une liste assez intéressante de Kata que je vous laisse le temps de découvrir.

On s’intéressera à un kata un peu particulier vu qu’il provient du monde des mathématiques et principalement de la calculabilité et la décidabilité à savoir le jeu de la vie.

Dans cet article, on présentera le jeu de la vie, l’histoire, l’origine et les règles. Ensuite, on commencera le développement en utilisant une approche fonctionnelle basé sur la TDD.

Bonne lecture…

Le jeu de la vie, l’origine et les règles

Le jeu de la vie ou Game Of Life est un automate cellulaire inventé par le mathématicien anglais John Conway en 1970. Le jeu se joue sur un échiquier infinie dont chaque cellule peut avoir deux états (vivant ou mort). On peut jouer tout seul en partant d’un état initial quelconque. Les règles sont très simples et on peut les résumer comme suit:

• Une cellule morte peut être vivante lorsqu’elle possède exactement 3 cellules voisines vivantes.
• Une cellule vivante peut devenir morte lorsqu’elle possède moins que deux cellules voisines vivantes (on parle d’un phénomène d’isolement ou underpopulation) ou plus de 3 cellules voisines vivantes(on parle de surpopulation)

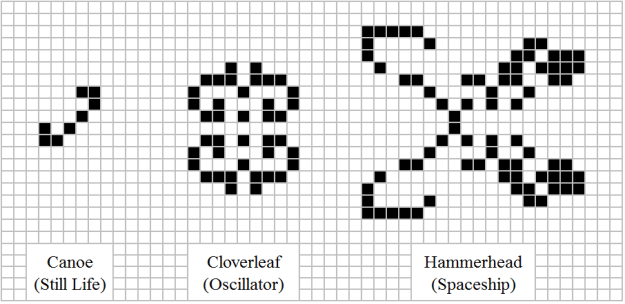
Le plus surprenant au sens mathématiques que Conway a pu dégager à partir de certains états initiaux et après certaines générations des formes stables que Conway les appels des natures mortes (serpent, oscillateur, pendule…). Le net est riche de plusieurs articles mathématiques qui cherchent à expliquer et comprendre comment on arrive à partir de ces deux règles simples à avoir ces formes.

Commençons le Kata

Essayons maintenant de penser une solution qui permet de résoudre d’une manière fonctionnelle et Swifty cet exercice.

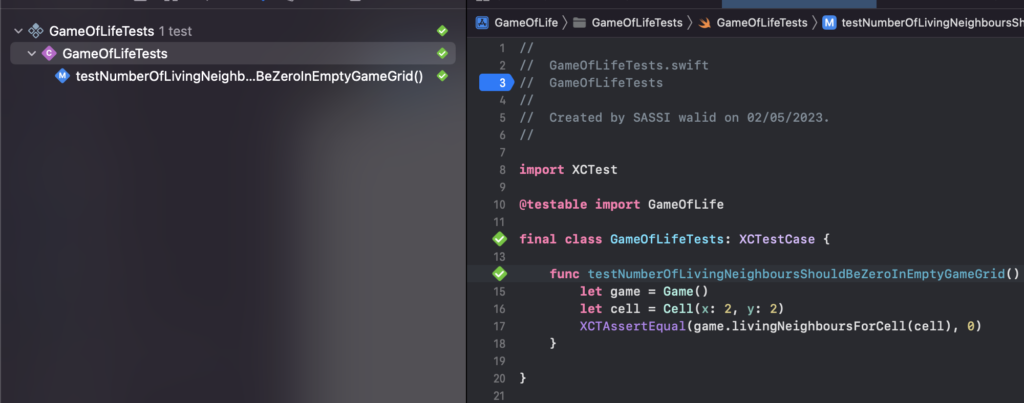
On peut commencer par un premier test qui permet de vérifier pour une grille de jeu composée d’une cellule morte, on peut pas trouver des voisins vivants.

On peut imaginer un test de ce genre:

final class GameOfLifeTests: XCTestCase {

    func testNumberOfLivingNeighboursShouldBeZeroInEmptyGameGrid() {
        let game = Game()
        let cell = Cell(x: 2, y: 2)
        XCTAssertEqual(game.livingNeighboursForCell(cell), 0)
    }

}

Nous pensons simplement à deux structures de données un jeu qu’on appelle Game et une cellule possédant deux coordonnées x et y. Le jeu doit être capable pour une cellule bien particulière, de calculer le nombre de ces voisins vivants

Commençons par la création de la classe ou la structure Game

final class Game {
    var cells: [Cell]

init() {
        cells = [Cell]()
    }
}

Puis la structure ou la classe Cell

final class Cell {

    let x: Int
    let y: Int
    
    init(x: Int, y: Int) {
        self.x = x
        self.y = y
    }
}

Pensons maintenant à implémenter une fonction ou une closure qui permet de calculer le nombre de cellules voisines vivantes par rapport à une cellule bien particulière. Pour répondre à cette question, on doit tout d’abord connaitre quels sont les cellules voisines?

ll y a cinq ans, on m’a proposé ce Kata comme test et je me suis bloqué sur la détermination des cellules voisines qui pour moi était la question la plus difficile 😃. Vu que nous sommes pas dans un entretien, essayons de penser calmement et trouver une bonne formule qui permet de déterminer les voisins.

On peut raisonner sur les indices des cellules et on remarquera que la différence en valeur absolue entre une cellule et ces voisins peut se résumer en ces trois cas au max (1,1),(1,0),(0,1). Comment on a aboutit à ça, regardons cette grille

En effet, si nous prenons par exemple, une cellule au milieu, la delta de différence entre sa position x et la position x de ses voisins ne dépassera pas 1 en valeur absolue et pareil pour sa position y. En effet, la cellule en haut à gauche et à une ligne de moins par rapport à notre cellule de milieu et une colonne de moins par rapport à notre cellule de milieu. Alors, on a cet offset de (-1,-1). On peut penser à une fonction qui cherchera les voisins en se basant sur cette logique et on aura:

private let cellsAreNeighbours = {
  (rhs:Cell, left: Cell) -> Bool in
  let delta = (left.x - rhs.x,left.y - rhs.y)
  switch delta {
  case (-1,-1),(-1,0),(-1,1),(0,-1),(0,1),(1,-1),(1,0),(1,1): return true
  default: return false
  }
}

Utilisons cette closure pour chercher les voisins d’une cellule quelconque

lazy var neighboursForCell = { (cell: Cell) -> [Cell] in
   self.cells.filter{ self.cellsAreNeighbours(cell, $0) }
}

Vous remarquez que l’écriture fonctionnelle rend notre code plus lisible vu qu’on utilise la fonction filtrer sur la séquence (tableau cells) afin de déterminer seulement les voisins. Autre chose, l’utilisation de la position x et y, nous évitera de créer une matrice et faire un parcours avec deux boucles. Alors notre parcours est toujours à O(n) en terme de complexité algorithmique temporelle.

Lançons notre premier test.

Passons à un deuxième test maintenant.

L’idée de ce deuxième test, c’est de vérifier pour une cellule bien particulière, qu’elle doit contenir après l’initialisation de jeu, un voisin vivant.

func testFoundOneLivingNeighbours() {
  let game = Game()
  let cell = Cell(x: 2, y: 2)
        
  game[2,1]?.state = .Alive
  XCTAssertEqual(game.livingNeighboursForCell(cell), 1)
}

Pour ce cas, la cellule (2,1) est voisine de la cellule (2,2). Comment peut on ajouter pour une cellule un état (state) et comment je peux accéder pour initialiser la cellule (2,1)?

Ecrivons le code qui permet d’ajouter l’attribut state à une cellule.

enum State {
    case Alive
    case Dead
}

final class Cell {

    let x: Int
    let y: Int
    var state: State
    
    init(x: Int, y: Int) {
        self.x = x
        self.y = y
    }
}

On a ajouté un type énuméré State qui contient 2 valeurs possibles:

• Vivant: Alive
• Mort: Dead

Surement, vous avez remarqué que je peux accéder à une cellule [x,y] en utilisant l’objet game et non pas faire game.cells[2,1]. En effet, j’utilise un subscript sur Game qui me permet d’accéder à une cellule de mon jeu directement.

subscript (x: Int, y: Int) -> Cell? {
   return cells.filter { $0.x == x && $0.y == y }.first
}

Les subscripts sont des raccourcis pour accéder au membres d’une classe, structure ou type énumère. On peut définir plus qu’un subscript sur un type. Dans notre example, le subscript permet de filtrer sur les cellules du Game et retourner une cellule dans les coordonnées sont égales à ceux passés en paramètres. Le résultat peut être nil, c’est pour cela on a ce type de retour Cell?.

Lançons notre deuxième test maintenant.

Dans le processus de développement TDD, il y a une étape très importante, c’est le refactoring (red -> Green -> refactor). Ce que nous pouvons remarqué dans la propriété cellsAreNeighbours qu’on peut améliorer la code en raisonnant en valeur absolue et on peut tomber sur 3 cas au lieu des 8 cas possibles

private let cellsAreNeighbours = {
   (rhs:Cell, left: Cell) -> Bool in
   let delta = (abs(left.x - rhs.x),abs(left.y - rhs.y))
   switch delta {
   case (1,1),(1,0),(0,1): return true
     default: return false
   }
}

Relancez les tests, normalement rien n’est cassé 🙂

On peut sécuriser notre code par l’ajout d’autres tests qui calcule le nombre de voisins pour une cellule s’il est égale à 2, 3…

func testFoundTwoLivingNeighbours() {

   let game = Game()

   let cell = Cell(x: 2, y: 2)

   game[2,1]?.state = .Alive

   game[2,3]?.state = .Alive

   XCTAssertEqual(game.livingNeighboursForCell(cell), 2)

}

Passons maintenant à la deuxième partie de notre Kata. La question qui se pose, comment je peux déterminer l’état de mon jeu pour la génération suivante.Il faut penser à implémenter le code qui permet de déterminer l’état de chaque cellule de jeu pour la génération suivante. Comme d’habitude, pensons au tests.

L’idée de notre test, si j’ai une cellule morte et qui est entourée de 3 cellules voisines vivantes, notre cellule deviendra vivante.

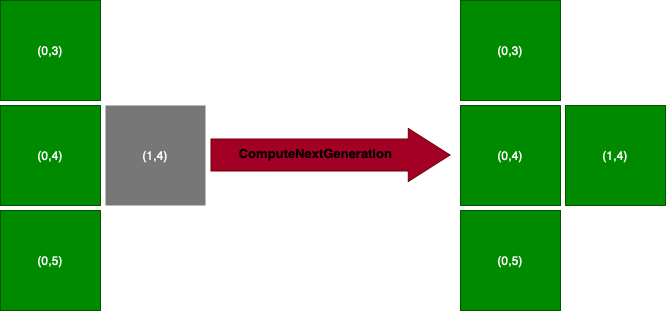
Notre test aura cette allure:

func testADeadCellWithThreeNeighboursGetsAlive() {
   let game = Game()
        
   game[0,3]?.state = .Alive
   game[0,4]?.state = .Alive
   game[0,5]?.state = .Alive
   game[1,4]?.state = .Dead
        
   game.computeNextGeneration()
        
   XCTAssertEqual(game[1,4]?.state, .Alive)
}

On est dans l’étape red en TDD, on doit penser à implémenter cette fonction computeNextGeneration().

On va s’intéresser tout d’abord à déterminer les cellules mortes, chercher ceux qui ont des voisins vivants puis appliquer une fonction de transformation pour avoir une nouvelle matrice de cells.

func computeNextGeneration() {
  let deadCells = cells.filter { $0.state == .Dead }

  let newLifeCells = deadCells.filter { livingNeighboursForCell($0) == 3 }
  // update state
  newLifeCells.forEach{ cell in
    cell.state = .Alive
  }
}

Vous remarquez que je change dans le tableau newLifeCells qui est une référence du tableau cells vu que notre Cell est une classe (chaque modification dans le newLifeCells impactera le tableau d’origine cells)

Lançons maintenant notre test.

Passons au test sur les cellules vivantes qui deviennent mortes suite à l’isolement ou la surpopulation.

Commençons par la surpopulation.

func func testACellWithMoreThanThreeLivedNeighboursDies() {
   let game = Game()
        
   game[0,3]?.state = .Alive
   game[0,4]?.state = .Alive
   game[0,5]?.state = .Alive
   game[1,3]?.state = .Alive
   game[1,4]?.state = .Alive
        
   game.computeNextGeneration()
        
   XCTAssertEqual(game[1,4]?.state, .Dead)
 }

La cellule (1,4) vivante deviendra morte dans la génération suivante. Ajoutons le code nécessaire pour faire cette transformation au niveau de la méthode computeNextGeneration()

func computeNextGeneration() {
.....
let liveCells = cells.filter{ $0.state == .Alive }
let dyingCells = liveCells.filter { livingNeighboursForCell($0) > 3 }

dyingCells.forEach{ cell in
    cell.state = .Dead
}

lançons notre test

Passons au test du cas d’isolement

func testACellWithLessThanTwoLivedNeighboursDies() {
   let game = Game()
        
   game[0,3]?.state = .Alive
   game[1,4]?.state = .Alive
        
   game.computeNextGeneration()
        
   XCTAssertEqual(game[1,4]?.state, .Dead)
}

Il suffit d’ajouter cette condition au niveau du filtre des cellules qui vont être mortes.

let dyingCells = liveCells.filter { livingNeighboursForCell($0) > 3 || livingNeighboursForCell($0) < 2 }

Conclusion

Le jeu de la vie constitue un Kata simple et intéressante pour perfectionner notre manière d’appréhender des problèmes algorithmiques et éventuellement se préparer pour des entretiens d’embauche. Dans cette première partie, nous avons présenté comment l’utilisation du TDD pour écrire petit à petit un code testable à 100% peut être si facile. Dans la partie suivante, nous allons s’intéresser à relier la logique algorithmique avec la création UI en utilisant UIKIT, et comment on peut améliorer notre solution en terme de complexité algorithmique.

A très bientôt.

Références:

Extreme programming explained: Kent Beck.

Software craftsmanship: Sandro Mancuso.

ARTE: Voyages au pays des maths: Le jeu de la vie

Le kata et le jeu : l’éducation par le jeu dans une « société sans cadre » ?